Skylor Blog

¶算法复杂度

算法复杂度分为时间复杂度和空间复杂度。
时间复杂度是指执行算法所需要的计算工作量；而空间复杂度是指执行这个算法所需要的内存空间。（算法的复杂性体现在运行某个算法时计算机所需资源的多少上，计算机资源最重要的是时间和空间（即寄存器）资源，因此复杂度分为时间和空间复杂度。）

¶时间复杂度

时间复杂度排序：
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n²logn) < O(n³)

简单快速判断算法的时间复杂度（适用于大部分简单的代码）

确定问题规模 n
循环减半过程 --> logn
k层关于n的循环 --> nᵏ
复杂情况 --> 根据算法执行过程判断

¶空间复杂度

空间复杂度：评估算法内存占用大小的式子
空间复杂度的表现方式和时间复杂度一致：

算法使用了几个变量： O(1)
算法使用了长度为n的以为列表： O(n)
算法使用了m行n列的二维列表： O(mn)
递归需要使用到系统栈的空间，因为需要记录上次递归中函数的位置，每走一层就需要消耗1个空间，所以没走k层，就需要消耗O(k)的空间

空间换时间

冒泡后选标记前插移位快归位(找到元素应有的位置)递归

import time

def cal_time(func):
    '''
    简易算法时间装饰器
    '''
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2-t1))
        return result
    return wrapper

以下所有的排序算法的实现，都是基于列表的下标完成的

¶递归问题

递归的特点： 1.调用自身 2.结束条件
递归案例：汉诺塔问题

def hanoi(n, a, b ,c):
    """
    n 表示圆盘个数
    三个参数代表三个柱子相对位置
    """
    if n > 0:
        hanoi(n-1, a, c, b)
        print('moving from %s to %s' %(a, c))
        hanoi(n-1, b, a, c)

hanoi(3, 'A', 'B', 'C')

算法解析：
为了保证小的盘子只能放在大的盘子之上，将n个盘子分为两个部分（1以及n-1两个部分），1 表示最后的一个大盘子，n-1 看作一个整体。

¶列表查找

列表查找（线性表查找）：从列表中查找指定元素

输入：列表、待查找元素
输出：元素下标（未找到元素时一般返回None或-1）

list类型内置查找函数：index() — 是线性（顺序）查找，因为二分查找要求列表是有序列表，故采用的是线性查找

¶顺序查找 (Linear Search)

也叫线性查找，从列表的第一个元素开始，顺序进行搜索

def linear_search(li, val):
    for ind, v in enumerate(li):
        if v == val:
            return ind
    else:                                       
        return None

时间复杂度：O(n)

python 中独创了 for...else... 以及 while...else... 语法，用于在循环结束之后直接执行else中的内容，好处是当循环中因为break退出时，else中的内容将不在执行。

¶二分查找 (Binary Search)

又叫折半查找，从有序列表的初始候选区 li[0:n] 开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

算法的前提：查找目标必须是排序好的列表

def binary_search(li, val):
    left = 0
    right = len(li) - 1
    while left <= right:
        mid = (left + right) // 2  
        if li[mid] == val:
            return mid
        elif li[mid] > val:
            right = mid - 1
        else:
            left = mid + 1
    else:  
        return None

时间复杂度：涉及到循环减半，所以复杂度是O(logn)

小结：
list类型内置查找函数index() 是线性（顺序）查找，因为二分查找要求列表是有序列表，故采用的是线性查找，
二分查找要求列表的顺序为有序列表，而排序算法的复杂度都大于O(n)，所以在选用查找方式的时候就需要斟酌：

有序列表，肯定采用二分查找（binary serarch）
无序列表，看查找的次数，如果查找只进行你一次，为了避免采用二分查找的列表排序的过程的消耗，推荐采用线性查找（linear search）
如果进行多次查找，可采用二分查找，此时排序的消耗时间可以忽略。

¶列表排序

将无序列表变成有序的列表

输入：列表
输出：有序列表

排序方式：升序与降序

内置排序函数： sort()

¶冒泡排序

冒泡排序的一趟过程：列表每两个相邻的数，如果前面比后面大，则交换两个数。（箭头只会到倒数第二个元素） —> 导致列表中的最大数的排到末尾。
最大值所在的区为有序区，剩下的为无序区，每一趟从无序区中得到一个最大值放到有序区中。
循环的次数（趟数）为列表长度n-1，因为最后一个元素不需要进行了。

代码的关键点：趟、无序区范围

def bubble_sort(li):
    for i in range(len(li)-1):  # 排序的趟数 = 总元素个数 - 1 因为剩下的最后一个元素(表首)不需要排序
        for j in range(len(li)-i-1):  # 总长度-有序区长度 - 1 = 无序区长度 -1 
            if li[j] > li[j+1]:  # 当前为升序排序，若降序则改为小于即可
                li[j], li[j+1] = li[j+1], li[j]

import random

li = [random.randint(0, 100) for i in range(10)]
print(li)
bubble_sort(li)
print(li)

时间复杂度： O(n²)

冒泡排序算法改进：
以上的实现中，默认是对所有的元素都进行了比较查看，
可能会存在的情况是说在一趟排序中，如[9, 8, 7, 1, 2, 3, 4]这样，在进行了3次冒泡之后，已经不需要再进行排序了，所以可以通过设置标记的方式将不在排序之后退出代码。

def bubble_sort(li):
    for i in range(len(li)-1):  
        exchange = False
        for j in range(len(li)-i-1): 
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                exchange = True
        if not exchange:
            return

算法改进（设置了标记值）之后，当列表值是顺序的时候，此时列表只会遍历一边，此时就达到了冒泡排序的最好情况时间复杂度 O(n)。

算法要点：每次循环找出并固定表尾的最大值。

¶选择排序

遍历列表，每次找出列表中的最小值，继续找剩下的列表中的最小值，即多次遍历列表，每次取最小数。

一般实现：

def select_sort_simple(li):
    li_new = []
    for i in range(len(li)):
        min_val = min(li)  # O(n)
        li_new.append(min_val)
        li.remove(min_val) # O(n)
    return li_new

算法的时间复杂度为 O(n²)，该算法虽然实现了选择排序的功能，但却另外开辟了内存空间，我们需要做到 原地排序 ，即不额外创建新的列表，而只在当前待排序的列表上进行操作。

改进方案：
将找出的小值从开头开始放，原先位置上的值与小值所在的位置进行交换。

def select_sort(li):
    for i in range(len(li)-1):  # i表示第几趟， 减少1 是最后剩下的一定是最大的数
        min_loc = i  # 将无序区第一个元素作为最小值进行比较，为了好进行位置交换操作，所以采用下标的形式
        for j in range(i+1, len(li)):  # 此处使用i+1作为第一个元素，去除了自己和自己比的过程
            if li[j] < li[min_loc]:
                min_loc = j  # 记录最小值的下标
        li[i], li[min_loc] = li[min_loc], li[i]

时间复杂度： O(n²)

算法要点：
每次得到表首的最小值，通过做标记，每次找出相对的较小值记录下标，一趟找出无序区的最小值与有序区某位交换位置。

¶插入排序

类似打牌插牌，初始手里（有序区）只有一张牌，每次（从无序区）摸一张牌，插入到手里已有牌的正确位置。

思路：
头部第一个数据为有序区第一个值，然后从第二个数据开始做为无序区提供的值（使用参数记录元素值，因为位置需要提供给有序区），与有序区中现有值进行比较，确定插入的位置，现有值按序挪动位置，占用无序区数据的位置。

挪位置的规则：从有序区最后一个值与待插入值进行大小比较，如果大于待插入值，则该元素移动（下标+1）

def insert_sort(li):
    for i in range(1, len(li)):  # i表示待插入的元素的下标
        tmp = li[i]  # 因为其所在位置要提供给有序区挪位，故记录
        j = i - 1  # j表示有序区最后元素的下标
        while j >= 0 and  li[j] > tmp :
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

时间复杂度： O(n²)

最好情况时间复杂度：O(n) 顺序情况，此时内部while不执行。

算法要点：和选择排序的起始下标不同，为1开始，因为默认0已经是有序区的最小值。

¶快速排序

思路：
取第一个元素p，使元素p归位（列表被分为两部分，左边都比p小，右边都比p大）。
递归完成所有元素的排序（左右两部分分别归位（归位时都是取部分的第一个值作为归位元素），直到归位元素一侧元素个数为1或者0），从而完成整个列表的排序。
所以，排序只要实现元素归位功能，然后递归即可。

快排算法框架：

def quick_sort(data, left, right):
    '''
    data 表示待排序的列表
    left 待排序列表的起始下标
    right 待排序列表的终点下标
    '''
    if left < right:  # 递归的终止条件，当左右相等的时候说明列表中只有一个元素，此时不需要进行排序
        mid = partition(data, left, right)  # mid 为归位元素的下标
        quick_sort(data, left, mid-1)
        quick_sort(data, mid+1, right)

归位算法实现：
归位，指回到其该有的位置（在排序后应该在的位置），实现步骤如下：

以列表的第一个值为待归位的元素（归位元素：使该元素左边的元素都是小于归位元素，右边的元素都大于归位元素），并记录该元素的值，此时列表产生一个空位。
从列表的最右边开始（因为步骤1选取列表第一个元素为待归位元素后，left指向的是待填补的空位），依次找小于待归位元素的值，没有就往前一个找，找到后，将元素放到空位left上，此时右边的位置提供了一个空位，然后从左边开始找大于待归位元素的元素，依次找大于待归位元素的值，找到后当到right空位上。
以此右边左边这样循环找，直到left=right，此时的空位为待归位元素的位置（最后必定是重叠的，都指向了归位元素所在的空位），保证了左边的元素都小于等于，右边都大于等于归位元素。

def partition(li, left, right):
    tmp = li[left]
    while left < right:  # 当两侧指针重叠，取消循环
        # 一定要先从右边开始找，因为此时左侧有空位
        while left < right and li[right] >=tmp:  # 从右边往左找
            right -= 1  # 一旦大于等于tmp，往左一步
        li[left] = li[right]  # 将右边找出的小的值放在空位上
        # 右边找到填补空位后，再从左边开始找填补右边的空位
        while left < right and li[left] <= tmp:
            left += 1
        li[right] = li[left]  # 左边的值填补到右边的空位上
    li[left] = tmp  # 循环结束后，此时left = right ，并且都指向了空位
    return left  # left 和 right 是同一个值

快速排序的时间复杂度：O(nlogn)

复杂度的粗略估计依据：

递归分层，对半分 n/2，每次减半，一共要分logn层，为 O(logn)
每层从全局上看是从左往右扫，扫描整个列表一次，所以每层的时间复杂度为 O(n)

所以时间复杂度是 O(nlogn)

空间复杂度：O(logn)
算法使用到了递归，递归需要消耗系统的内存资源，考虑平均情况下递归分层为 logn 层，所以使用空间复杂度为 O(logn)。

快速排序的问题，递归：

python有递归最大深度的限制（可以更改），默认的递归深度是有限制的，当递归深度超过默认值的时候，就会引发RuntimeError。
递归深度解决方式：
1
2
import sys
sys.setrecursionlimit(1000000) # 表示递归深度为100w
递归会消耗相当大的系统资源 — 内存

快速排序最坏情况：
好的情况下每次分层都是能够对半分 n/2，所以分层要分logn层，为 O(logn) ，但是最坏的情况，如 [5,4,3,2,1] 这种有顺序的列表，当前算法选取的left每次都是最大值，会导致分层的时候不是对半分，而是分为 1 和 n-1 两个部分，这就导致递归分层是的层数和 n 相同，此时分层的时间复杂度为 O(n)，所以最坏的情况下的时间复杂度为 O(n²)。同理，此时对应的最坏空间复杂度就为O(n)。

解决措施：为了避免有序的列表使用快排产生的问题，此时可以使用 随机主元 的方式，即随机选取需要归位的元素，而非使用left位置的元素，这样可以一定程度上减轻倒序列表的影响。

import random

def random_partition(li, left, right):
    i = random.randint(left, right)  # 随机产生需要归位的元素下标
    tmp = li[i]
    while left < right:
        while right > i and li[right] >= tmp:
            right -= 1
        li[i] = li[right]
        i = right  # 将i指向新的空位

        while left < i and li[left] <= tmp:
            left += 1
        li[i] = li[left]
        i = left
    li[i] = tmp
    return i

通过运行时间分析，在处理倒序列表时，性能提升到处理一般数据的性能，在常规列表的测试下，性能与选取left位置元素相差无几。

算法要点：配合动画理解
判断的标准始终是左边指针小于右指针，i始终指向的是空位。
默认采用的以左边第一个为待归位值，实际上是一种特殊的情况，在代码实现中left和right即作为了元素指针，又作为空位指针。

¶堆排序

¶树和二叉树

树是一种数据结构
一些概念：

节点的度：表示某个节点的分叉个数
树的度：书中度最多的节点的度为树的度

二叉树定义：

度不超多2的树
每个节点最多有两个孩子节点

完全二叉树：叶节点只能出现在最下层和次下层，并且最下层的节点都集中在该层最左边的若干位置的二叉树。
满二叉树：一个二叉树，如果每一层的节点数都达到最大值，则这个二叉树就是满二叉树，满二叉树是特殊的完全二叉树。

二叉树的存储方式：

链式存储方式
顺序存储方式：使用列表来存储

完全二叉树父节点和左孩子节点的编号下标的关系： i -> 2i+1 (i从0开始)
完全二叉树父节点和左孩子节点的编号下标的关系： i -> 2i+2 (i从0开始)
反之，从孩子节点找父节点都可以采用 (孩子节点编号-1)//2 ，注意使用的是整除。

¶堆

一种特殊的完全二叉树。
大根堆：一个完全二叉树，满足任一父节点都比其他孩子节点大。
小根堆：一个完全二叉树，满足任一父节点都比其他孩子节点小。

升序排序采用大根堆排序，利用堆的向下调整的性质实现。
向下调整性质：
当根节点的左右子树都已经是堆（假设是最大值）的时候，但根不满足堆，可以通过一次向下的调整来将其变成一个堆。
向下调整原理：
根节点不是最大值，从其两个子节点中选取较大的值替换现在的根节点（选两者的较大值保证了堆的性质，能保证根大于孩子节点），出现的空位再使用空位节点的两个子节点以及之前的根节点中的较大值最为根节点值替换，以此类推，最后的空位使用出来的变量替换。

堆排序的过程：

建立一个堆（升序使用的大根堆）。
得到堆顶的元素，为当前数据中的最大值。
去除堆顶，将堆的最后一个叶子结点（选取最后一个叶子节点，是为了保证经过调整之后，最后得到的树是一个完全二叉树）的元素放到堆顶，此时可通过一次调整性质得到大根堆。
将堆顶元素抛出，为当前数据中的第二大值。
重复步骤3，直到堆为空。

堆的构造：
一个完全二叉树，从最后一个非叶子节点开始，对每个小的子树进行向下调整，最后得到的就是一个堆。

¶堆排序代码实现

算法实现：

def sift(li, low, high):
    """
    大根堆向下调整实现
    注意对的前提是此堆除了堆顶外，其他部分已经满足大根堆

    :param li: 列表
    :param low: 堆的根节点
    :param high： 堆的最后一个元素的位置
    :return
    """
    i = low  # 开始指向根节点
    j = 2 * i + 1  # 开始指向左孩子节点
    tmp = li[low]  # 将堆顶元素存储
    while j <= high:  # 只要j没有越界，就表示i指向的节点不是叶子节点
        if j + 1 <= high and li[j+1] > li[j]:  # 如果有右孩子节点，且相对较大
            j = j + 1  # 将j指向右孩子
        if li[j] > tmp:
            li[i] = li[j]  # 直接兑换，因为以j为根的子树已经是大根堆，所以li[j]此时已经是最大的了
            i = j  # 同理，指向下一层，执行同样的步骤，为tmp找位置
            j = i * 2 + 1
        else: 
            break
    li[i] = tmp


def heap_sort(li):
    # 首先构造一个大根堆
    n = len(li)
    for i in range((n-2)//2, -1, -1):  # 倒推，从最后一个父节点开始找所有的父节点
        # i表示建堆开始的时候调整的部分的根的下标
        sift(li, i, n-1)  # 从最后一个堆开始，每个小堆都可以使用向下调整得到大根堆，循环结束后，整个大根堆构造完成
        # 传递的high参数使用了一个小技巧
    # 开始挨个提出大根堆堆顶元素
    for i in range(n-1, 0, -1):  # 从最后一个元素开始，用于替换为树的根节点，剩下的最后一个不需要进行调整，所以到0即可
        li[0], li[i] = li[i], li[0]  # 堆顶和最后一个元素交换，存储堆顶最大值，将最后一个叶子节点值放到堆顶开始调整
        sift(li, 0, i-1)

时间复杂度：O(nlogn)
其中，sift()函数的时间复杂度为O(logn)，这是因为最坏的情况需要进行二叉树的深度次数大概是logn，即当前完全二叉树的根值需要放到最底层的叶子节点位置才完成了大根堆。

实际表现堆排序相对快速排序要稍微慢一些。

¶heapq模块

python内置的堆排序模块heapq，其中的 _siftdown() 方法实现的就是向下调整。
heapq 表示的意思是 heap queue , 即用堆实现的优先队列（优先队列指小的元素先出，或者大的元素先出）。
使用：

import heapq
import random

li = list(range(100))
random.shuffle(li)


heapq.heapify(li)  # 建堆，建造一个小根堆

print(heapq.heappop(li))  # 往外弹出一个最小的元素

¶堆的思想的应用

topk 问题：现有n个数，设计算法得到前k大的数（k < n）。
解决该问题的几种方式：

排序后进行切片 O(nlogn)，k < n，此处忽略切片的复杂度 O(k)，只考虑了排序的时间复杂度（排序采用时间复杂度更低的快排或者堆排）。
使用复杂度为 O(n²) 的排序算法，但只进行k次排序（因为topk问题只要前k大的数），总的时间复杂度为 O(kn)，当数据多，k小的时候，该算法明显优于方法1。
采用堆，思路和堆排序的实现类似，但是堆的元素只有k个，时间复杂度为 O(nlogk)。

使用堆解决 topk 问题思路：

取列表前 k 个元素建立一个 小根堆，堆顶就是目前第 k 大的数（ k 个元素中的最小的那个元素）。
依次向后遍历原列表，将列表中的元素与当前小根堆的堆顶元素比较，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素（此时堆内的元素就是目前 k 个最大的元素，堆顶是 k 个元素中最小的），并且对堆进行依次调整。
遍历列表所有元素后，倒序弹出堆顶元素。

topk 问题一定要采用小根堆，因为堆中元素的大小关系，只能保证的是堆顶元素一定是最大的（使用大根堆）或者最小的（使用小根堆）。

此方式的时间复杂度为 O(nlogk)，需要遍历所有的数 n，但是堆的元素个数始终只有 k 个，所以此时 sift() 函数的时间复杂度和 k 相关，为O(logk)，所以使用堆解决 topk 的时间复杂度为O(nlogk)

代码实现：

def sift(li, low, high):
    """
    小根堆向下调整
    """
    i = low  
    j = 2 * i + 1  
    tmp = li[low] 
    while j <= high:  
        if j + 1 <= high and li[j+1] < li[j]:  
            j = j + 1  
        if li[j] < tmp:
            li[i] = li[j]
            i = j  
            j = i * 2 + 1
        else: 
            break
    li[i] = tmp

def topk(li, k):
    heap = li[0:k]
    # 建堆
    for i in range((k-2)//2, -1, -1):
        sift(heap, i, k-1)
    # 遍历列表剩余元素，如果比堆顶元素大，就替换并重新调整小根堆
    print('最初的根堆：', heap)
    for i in range(k, len(li)):
        print(i)
        if li[i] > heap[0]:
            heap[0] = li[i]
            sift(heap, 0, k-1)
        print('小排序：', heap)
    print('完成：', heap)
    # 倒序输出堆中的元素
    for i in range(k-1, 0, -1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i-1)
    return heap

¶归并排序

归并：将两个有序的列表合并为一个有序的列表

归并排序步骤：

分解：将列表越分越小，直至分成一个元素为一个列表。
终止条件：一个元素是有序的。
合并：将两个有序列表归并，列表越来越大。

算法实现：

def merge(li, low, mid, high):
    '''
    归并
    '''
    i = low
    j = mid + 1
    ltmp = []  #  设置临时变量
    while i<= mid and j <= high:  # 只要左右两边都有数
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    # while执行完，两部分肯定有一部分是没有值的
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp

def merge_sort(li, low, high):
    if low < high:  # 至少有两个元素，递归，只有一个元素时不需要处理
        mid = (low+high) // 2
        merge_sort(li, low, mid)
        merge_sort(li, mid+1, high)
        merge(li, low, mid, high)  # 通过递归，此函数第一次执行的时候，一定是两个各位1个元素的列表的集合。

时间复杂度：O(nlogn)
空间复杂度：O(n)
之前的排序都是原地排序，但是归并排序需要使用一个中间列表存储一次归并后的列表，所以需要使用额外的空间，需要考虑空间复杂度

Python 内置的 list.sort() 方法内部实现是基于归并排序的 TimSort 排序算法，是结合了归并排序以及插入排序的排序算法。

¶小结

一般情况下，就运行时间而言：
快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：

快速排序：极端情况下（倒序）效率低，为 O(n²)。
归并排序：需要额外的内存开销。
堆排序：在快的排序算法中相对较慢。

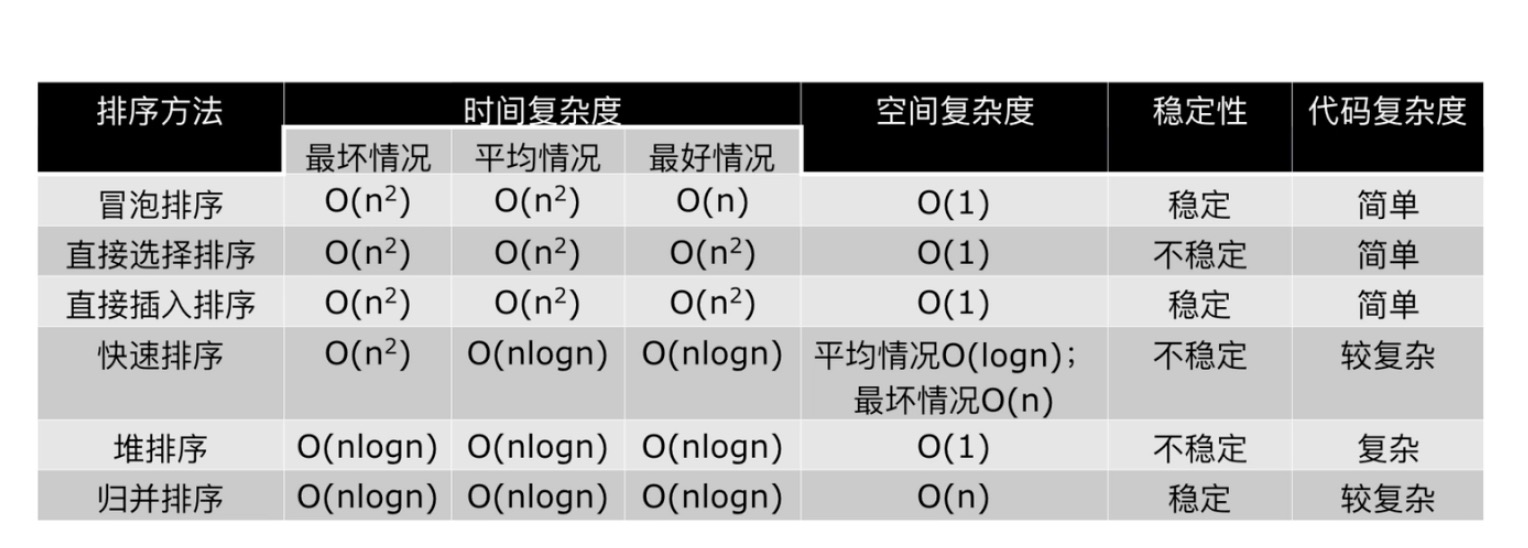
排序的稳定性：当两个元素的值一样的时候，保证他们的相对位置不变。
一般的，挨个比较的都是稳定的，如冒泡排序、插入排序、归并排序等。

¶希尔排序

由插入排序变形而来，是一种分组插入排序。
步骤：

首先取一个整数d𝟭=n/2，将元素分为d𝟭个组，每组相邻两个元素之间的距离为 d𝟭，在各组内进行直接插入排序。
取第二个整数d𝟮=d𝟭/2，重复上述分组排序过程，直到d𝐢=1，即所有元素在同一个组内进行直接插入排序。

希尔排序每趟并不使元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

实现代码：

def insert_sort_gap(li, gap):
    for i in range(gap, len(li)):
        tmp = li[i]
        j = i- gap
        while j >= 0 and li[j] > tmp:
            li[j+gap] = li[j]
            j -= gap
        li[j+gap] = tmp

def shell_sort(li):
    d = len(li) // 2
    while d >= 1:
        insert_sort_gap(li, d)
        d //= 2

和插入排序的性能对比：强于普通的插入排序，稍慢于堆排序（所以也比快速排序以及归并排序慢）

希尔排序的时间复杂度：没有明确的值，取决于 gap 的选择，不同的 gap，得到的时间复杂度也不相同，我们选取的 gap 为 N/2ᴷ，时间复杂度介于 O(nlogn) 和 O(n²) 之间。

¶计数排序

是一个非基于比较的排序算法。
前提条件是，需要知晓待排序的列表中的元素值的范围。

解决诸如以下问题：
对列表进行排序，已知列表中数的范围都在0到100之间，设计时间复杂度为O(n)的排序算法。

实现代码：

def count_sort(li, max_count=100):
    count = [0 for _ in range(max_count+1)]  # 建立一个用于计数的列表，列表的下标用于记录数，下标上的值作为统计的个数
    for val in li:
        count[val] += 1
    li.clear()  # 使用原先的列表空间作为排序后的列表空间
    for ind, val in enumerate(count):  # 操作的对象不是n(这里的排序对象li），所以不参与时间复杂度计算，涉及到n的部分实际上就是li.append(ind)的过程，为O(n)，所以整体的时间复杂度为O(n)
        for _ in range(val):  
            li.append(ind)
import random

li = [random.randint(0,100) for _ in range(1000)]
count_sort(li)
print(li)

它的优势在于在对一定范围内的整数排序时，它的复杂度为 Ο(n+k)（其中k是整数的范围），快于其他任何的 比较排序 算法。当然这是一种牺牲空间换取时间的做法，而且当 O(k)>O(nlog(n)) 的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是 O(nlog(n)), 如归并排序，堆排序）。

¶桶排序

在计数排序中，如果元素范围比较大，为了构造相应的列表就会消耗大量的资源，此时可以使用桶排序的方式进行改造(避免了未存在的元素占用列表空间)。
桶排序（Bucket Sort）：首先将元素分在不同的桶中，再对每个桶中元素进行排序。

实现代码：

# 桶排序
def bucket_sort(li, n=100, max_num=10000):
    """
    n : 桶的个数
    max_num: 所有的数中的最大值
    """
    bucketes = [[] for _ in range(n)]  # 创建桶
    for var in li:  # 数据入桶
        i = min(var // (max_num//n), n-1) # i 表示 var 放到几号桶里，桶号从0开始
        # 使用min(.., n-1)是为了处理临界情况，超过的数放到最后的桶中
        bucketes[i].append(var)
        for j in range(len(bucketes[i])-1, 0, -1):
            if bucketes[i][j] < bucketes[i][j-1]:
                bucketes[i][j], bucketes[i][j-1] = bucketes[i][j-1], bucketes[i][j]
            else:
                break
    sorted_li = []
    for buc in bucketes:
        # sorted_li += buc
        sorted_li.extend(buc)
    return sorted_li

分析：
代码的核心内容是i = min(var // (max_num//n), n-1) ，该语句巧妙的完成了分桶以及数据的入桶，这是一种平均情况下的分桶策略，对于如果数据分布集中的情况下，可以对集中部分的桶再进行分桶，这取决于具体的数据情况。
分桶的桶的数量取决于数据中的最大值。

桶排序的表现取决于数据的分布，假使大部分的数据都集中在一个桶中，则性能就取决于一个桶的排序性能，而我们使用桶排序的目的是为了将数据分散在不同的桶中，每个桶中存储等量较少值，然后对较少的值进行排序，这样排序性能才会有所提升。也就是需要对不同数据排序时采取不同的分桶策略。

平均情况的时间复杂度：O(n+k)
最坏情况时间复杂度：O(n²k)
空间复杂度：O(nk)
*k 通过n和m算出（n表示数据的个数，m表示桶的个数），k表示一个桶的大小。

优化建议：桶内数据的排序方式、不同数据分布下，分桶的策略。

¶基数排序

类似关键字排序，基于桶排序，但是不使用桶内排序，而是借助桶的顺序（0-9的桶），完成每个数位上的数值大小的排序，从而实现所有数据的排序。

代码实现：

# 基数排序
def radix_sort(li):
    max_num = max(li)  # 最大值的位数决定了循环的次数
    it = 0
    while 10 ** it <= max_num:
        buckets = [[] for _ in range(10)]
        for var in li:
            digit = (var // 10 ** it) % 10
            buckets[digit].append(var)
        # 分桶完成
        li.clear()
        for buc in buckets:
            li.extend(buc)  # 把数据直接写会原来的数组，此时数组已经完成了个位数的排序，然后继续执行十位数的排序，依次进行。
        it += 1

关键点：没有使用内部排序，而是借助0-9的桶的相对位置来完成数据的排序。
时间复杂度：O(kn)
空间复杂度：O(k+n)
k表示数字的位数，代码中的it。

分析：基数排序的时间复杂度是线性的，相比于非线性的快速排序，在特定的情况下的数据

Skylor Blog

RabbitMQ 基础部分

Celery 基本使用

Ajax 跨域问题解决方案

Flask和Django的密文生成分析--厉害的PBKDF2

不再安全的SHA-1

信息摘要算法的python实现和使用场景

UUID的python实现

Python 元类编程思考

¶什么是元类

¶使用type动态的创建类

算法数据结构

¶算法复杂度

¶时间复杂度

¶空间复杂度

¶递归问题

¶列表查找

¶顺序查找 (Linear Search)

¶二分查找 (Binary Search)

¶列表排序

¶冒泡排序

¶选择排序

¶插入排序

¶快速排序

¶堆排序

¶树和二叉树

¶堆

¶堆排序代码实现

¶heapq模块

¶堆的思想的应用

¶归并排序

¶小结

¶希尔排序

¶计数排序

¶桶排序

¶基数排序

¶

Base64 编码